
이렇게 3개의 알고리즘을 하나로 묶은 이유는, 모두 최단 경로를 찾는 알고리즘이기 때문입니다.
최단 경로 문제
- 시작점, 끝점이 정해져있음.
- 가중 그래프가 주어졌을 때, 최단 경로를 구해야 합니다.
벨만-포드(Belman-Ford) 알고리즘
- 음수 비용이 있을 경우에도 사용 가능합니다.
- 첫 위치를 0로, 나머지 위치를 ∞로 설정해 놓는다.
ex) A에서 G로 갈때, 최단 경로를 구하시오.
1) A를 0으로, 나머지를 ∞로 설정합니다.
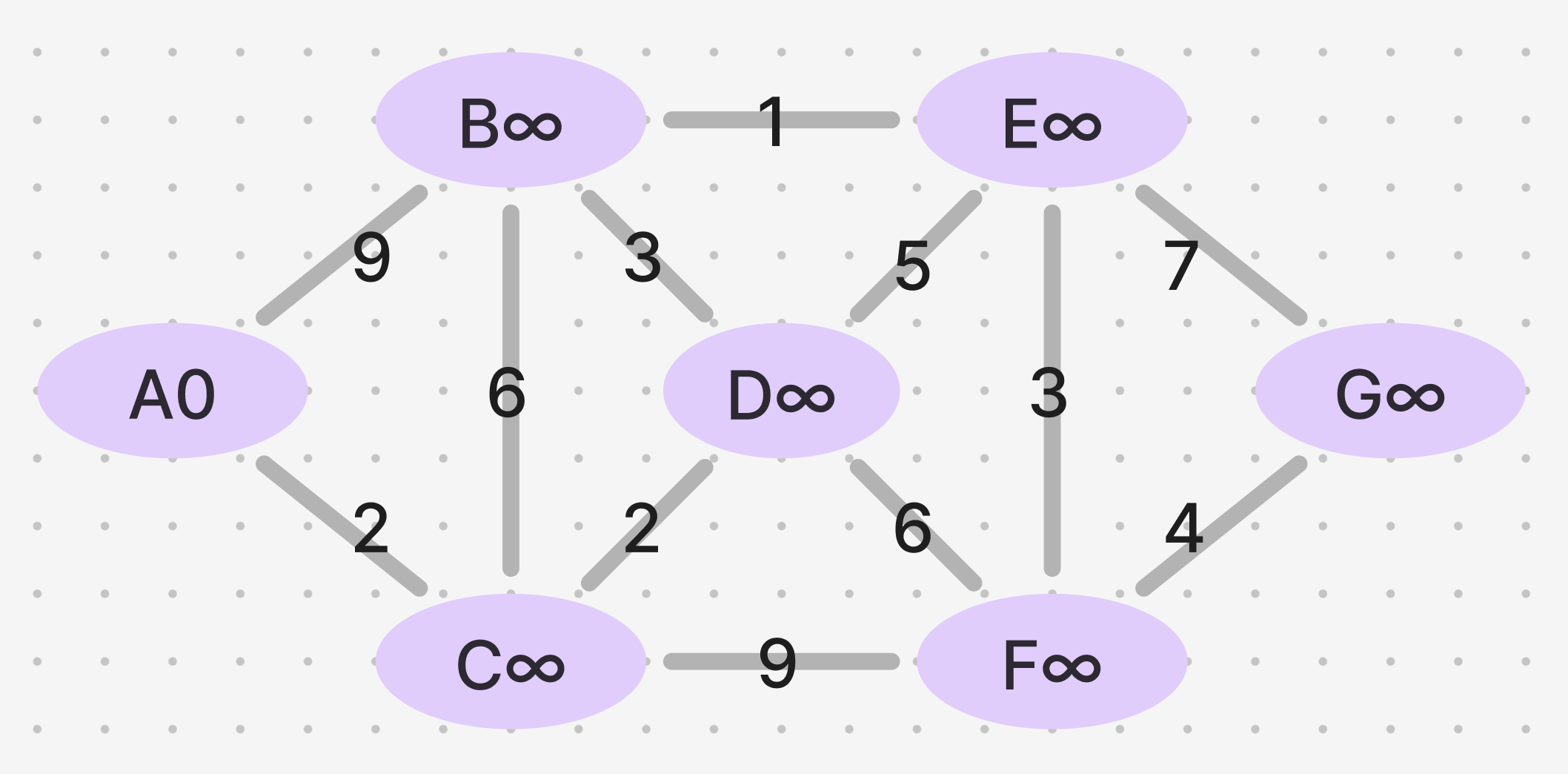
2) 간선(A-B)을 골라 거리를 구합니다. (B : 9, A: 0)


2) 또 다른 간선(A-C)을 구해 최단 거리를 구합니다. (C: 2)


3) 또 다른 간선(B-C)를 구해 최단 거리를 구합니다. (B : 8)

4) 또 다른 간선(B-E), (B-D)을 구해 최단 거리를 구합니다. (D: 11, E: 9)

5) 또 다른 간선(C-D), (C-F)을 구해 최단 거리를 구합니다. (D: 4, F: 11)

6) 또 다른 간선(D-F)을 구해 최단 거리를 구합니다. (F: 10)

7) 모든 다른 간선을 구해 최단 거리를 구합니다. (G: 14)

8) 두번째 사이클 : 더이상 변경이 없을 때 까지 처음부터 간선들을 선택하며 사이클을 돌립니다. (B: 7, E: 8)

9) 세번째 사이클 : 두번째 사이클에서 변경사항이 있었으므로, 세번째 사이클을 돌리며 변경사항이 존재하는지 확인합니다.
더 이상 변경사항이 없기 때문에 사이클을 종료합니다.
결론 : A에서 G까지의 최단 경로는 A-C-D-F-G이고, 비용은 14입니다.
정점 수 : n, 간선 수 : m이라 했을 때,
- 한 차례의 갱신 작업은 간선 하나를 조사하므로 O(m)만큼 걸립니다.
- 비용 갱신 작업을 n차례 수행하면 끝납니다. O(n)
결과 : 시간복잡도 O(nm)
* 비용이 음수일 경우에도 동작하지만, 페로(사이클)이 존재하는 경우, n회 반복했을 때도 계속 변경사항이 있는 경우는 최단경로가 존재하지 않습니다.
다익스트라(Dijkstra) 알고리즘
- 음수 비용일 경우 완벽하지 않아서 벨만포드를 사용합니다.
- 벨만포드 알고리즘은 사이클 한번 당 수정작업이 없을 경우 끝나기 때문에 시간이 오래 걸리는 반면, 다익스트라는 정점에 대해 작업을 하기 때문에 한 사이클만 돌면 끝나서 효율적입니다.
- 후보 정점들 중 가장 값이 작은 정점을 선택하여 다음 단계를 돌립니다.
ex) A 정점에서 G 정점까지의 최단 경로를 구하시오.

1) A정점의 값을 0이라 하고, A 정점에서 연결된 정점들에 대한 값을 변경할 수 있으면 변경해줍니다. (B -> 2, C -> 5)

2) 초록색 정점들(다음 후보지) 중에서 값이 가장 작은 정점을 골라 연결합니다(주황색).

3) 이제 B에서 연결된 정점들 중 값을 변경할 수 있으면 변경해줍니다. (C는 5<8이므로 변경 X, D -> 3, E -> 5)

4) 초록 정점들 중 가장 값이 작은 정점을 고릅니다. (D가 가장 작으므로 D 선택)

5) D에 연결된 정점들 중 변경 가능한 정점의 값을 수정하시오. (E : 5<7 이므로 변경 X)
그 후, 가장 작은 값인 C를 연결.
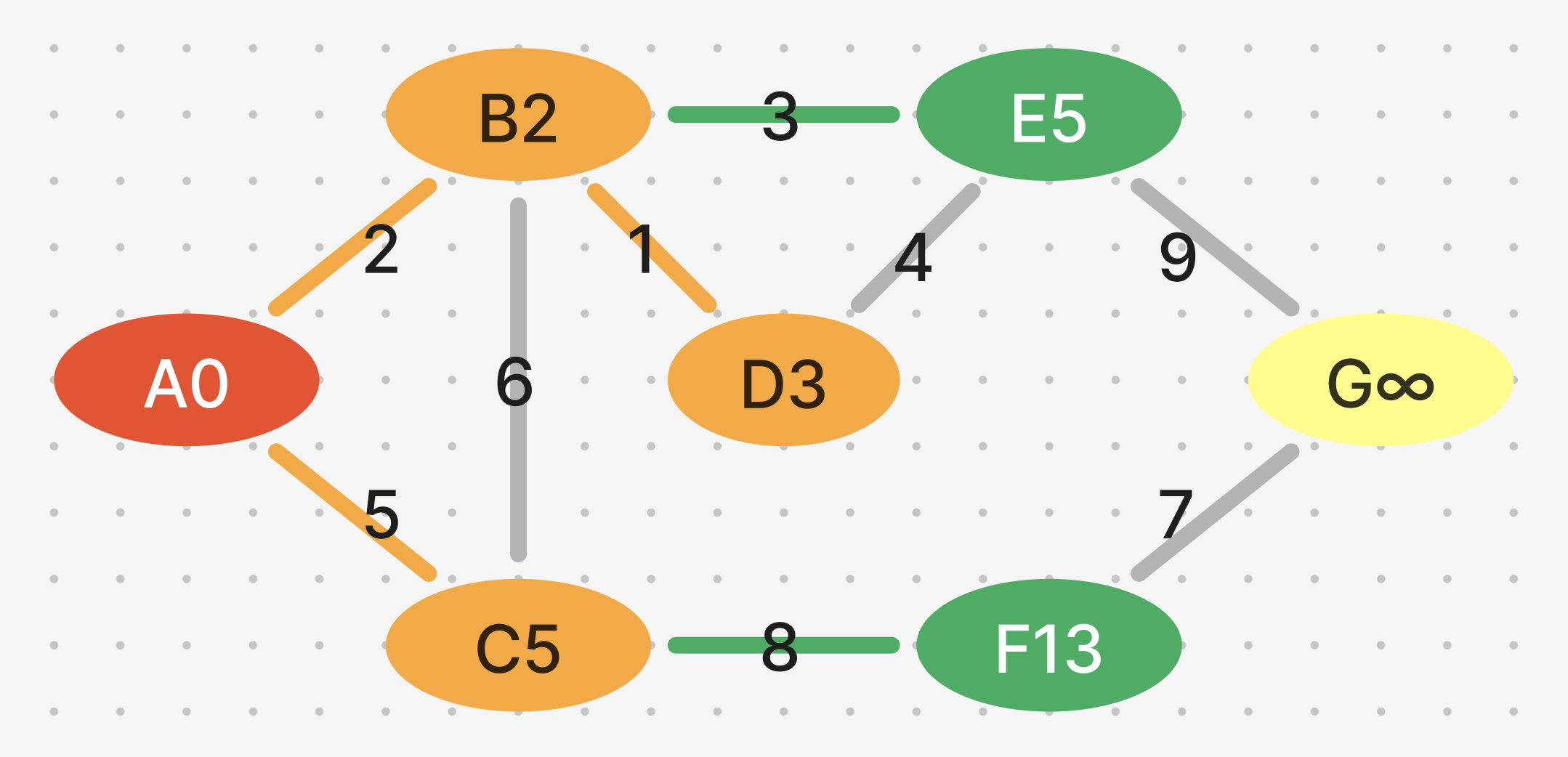
6) C에서 연결된 정점 중 변경 가능한 정점의 값을 수정하시오. (F : 13)
연결된 정점 중 값이 가장 작은 정점을 선택합니다. (E)

7) E와 연결된 정점 중 변경 가능한 정점의 값을 수정하시오. (G : 14)
연결된 정점 중 값이 가장 작은 정점을 선택합니다. (F)

8) F와 연결된 정점 중 변경 가능한 정점의 값을 수정하시오. (변경사항 X)
연결된 정점 중 값이 가장 작은 정점을 선택합니다. (G)

9) (노란색)이런 식의 연결 구조가 형성됨.
최단 거리는 14이고, 최단 경로는 A-B-E-G입니다.

- 시간 복잡도는 O (m + n log n) 입니다.
'CS 지식 > 자료구조_알고리즘' 카테고리의 다른 글
| 최소 신장 트리(MST) : 크루스칼(Kruskal) & 프림(Prim) (0) | 2025.01.15 |
|---|---|
| 그래프(Graph) : 너비우선탐색(BFS) & 깊이우선탐색(DFS) (0) | 2025.01.13 |
| 이진 탐색 (Binary Search) (0) | 2025.01.13 |
| 힙 정렬(Heap Sort), 병합 정렬(Merge Sort), 퀵 정렬(Quick Sort) (0) | 2025.01.12 |
| 버블 정렬(Bubble Sort) vs 선택정렬(Selection Sort) vs 삽입정렬(Insertion Sort) (0) | 2025.01.11 |


댓글